海上风电电缆故障定位的优化算法研究
2018-07-25 09:21 [新能源论文] 来源于：互联网 作者： 陈灿
导读：【摘要】针对并网的海上风电场发生海底电缆故障时，难于巡线以及参数测量误差太大等困难，本文提出了一种利用海上和陆上变流站的电流电压频谱信息对故障位置进行优化辨识的算法。本文首先建立海上风电场线路模型，并基于集中参数模型确定测距观测方程，同时
|
【摘要】针对并网的海上风电场发生海底电缆故障时，难于巡线以及参数测量误差太大等困难，本文提出了一种利用海上和陆上变流站的电流电压频谱信息对故障位置进行优化辨识的算法。本文首先建立海上风电场线路模型，并基于集中参数模型确定测距观测方程，同时引入误差归一化构建定位最优化模型，最后将电流电压的频谱分量代入优化模型并用模拟退火算法求解。PSCAD仿真结果表明算法基本满足海上风电场海底电缆故障定位要求。
【关键词】海底电缆；故障定位；频域法；模拟退火法；优化算法
1.引言
随着全球经济的不断发展，能源危机也越发严重。传统能源因其储量有限、污染太大等原因促使人们不断开发新能源。风能作为一种可再生的清洁能源在全球范围内储量丰富，加之土地资源日益紧缺、近海地域风储量富足，大力发展海上风电已成为解决能源危机的一个重要手段[1]。
然而由于海域的海况及地质环境复杂，海床塌陷、局部滑坡、海浪和海流以及船只抛锚对海底电缆造成的损伤和断裂事故时有发生，影响了海上安全生产。根据丹麦海上风电场运行经验：海上风电场寿命一般为20年，此期间海底电缆故障率一般为0.32次/（100km·年）[6]，电缆填埋后的典型故障率可以达到0.1次/（100km·年）。一旦海底电缆发生故障就会导致部分风机不能正常发电，一方面会增加故障维修的费用，另一方面风电场在故障维修期间还会损失发电的收入。由于电力电缆都有厚的绝缘层，又埋于海底，一旦发生故障，寻找起来将十分困难，往往需要花费大量的人力、物力[2]。因此，准确的故障定位对于快速查找故障点、减轻故障巡线负担、减少停电检修时间、以及提高海上风电场的供电可靠性具有十分重要的意义。
为寻求快捷、准确的电缆故障点监测和定位方法，国内外电力科技工作者付出了不懈的努力。行波法在线故障测距的应用前景较乐观，但仍有很多技术难题需要解决[3-12]。本文提出了一种频域优化测距方法。基于海底电缆的集中参数模型，并在测距观测方程中将电缆参数作为未知估计量，然后选取不同的频谱分量列出其相应的网络方程。算法以各频谱满足的网络方程作为约束，以末端电网侧电压估计值与实测值间的误差最小作为优化目标函数。并在确定目标函数中，引入归一化因子选择各频谱误差的权重，建立海底电缆故障测距优化模型。算法不受参数测量误差的影响，而且引入频谱较宽，理论上可以达到非常高的精度，对海底电缆故障定位较为实用可靠。最后利用模拟退火算法求解并基于Matlab和PSCAD进行了仿真计算。
2.故障测距原理
2.1 故障网络方程的建立
图1所示为海底电缆输电线路发生故障时的网络模型，故障数据采集装置安装于海上变电站m和路上变电站n两端，f为故障点，Im和In为故障电流。考虑到电力系统中大多数超高压输电线路都是平衡系统或接近平衡系统，而且正序分量在任何故障类型下均存在，因此，本文采用正序分量系统[13]进行故障测距。
海底电缆发生故障后，根据电缆两端采集到的故障频谱信息列出故障点电压：
（1）
（2）
上述式子中，x为故障点离首端的距离，D为海底电缆总长度，为待识别参数。Z、Y为海底电缆的串联阻抗和并联导纳：
（3）
式中R、L、C分别为海底电缆集中参数模型中的电阻、电感和电容，均为待识别参数。故障点处电压相等，则可以得到故障测距方程：
（4）
2.2 故障频谱方程的建立
式（4）为故障测距方程，共有4个未知参数：D、R、L、C，因此，要解出故障距离x，至少要5个方程。根据线性系统理论，线路中各点暂态响应电流、电压的频谱是连续的，对于任意给定的频率，均可对故障网络写出相应的频谱方程[13]。所以故障电压电流中的谐波信号也符合故障测距方程。为此，方程（4）可转变为：
（5）
式中： （6）
3.故障测距优化模型
故障测距的研究目标是在海上风电并网系统发生故障时能准确查找故障点。为此需要寻求一种算法，使得出的估计值与实际值间的误差最小。这就形成最优化问题：在电缆线路参数及其网络方程的约束下，寻求使测距总误差最小的决策。因此，本文引用最优化的思想，建立故障测距优化模型，使测距精度最高。
由线性系统理论可知，各谐波均满足网络方程，未知参数有4个，加上故障距离x，理论上只需5个方程即可求解。但考虑到各种主客观因素，无法避免的误差（仪器测量、频域变换软件等），定位结果仍不够精确。为此，我们通过提取较多的频谱信息，并分解实部和虚部，构建裕量方程组求解。基于上述考虑，本文以总测距误差最小为优化目标，并赋予各谐波误差合适的权重，构建了以下的故障测距优化模型。
以电缆末端路上变电站电压为误差评价基准，提取出，使方程（5）转化为：
（7）
令则方程变为：
（8）
对任一组参数D、R、L、C，线路末端电压的误差为：
（9）
式中，为实测值
将上式拆分为实部和虚部两个方程，误差分别为、
本文提取故障的基波、2次、3次与4次谐波信号，以各频谱电缆末端电压的误差平方和为优化目标函数，建立误差优化模型。
（10）
式中：w1、w2、w3、w4分别为基波、二次谐波、三次谐波、四次谐波电压误差相应的权重。这是一个多目标优化函数问题，由于频谱能量分布不均，谐波含量很低，与基波幅值存在数量级的差别，为此，考虑权系数与各谐波幅值成反比，使其变为相对误差，将谐波能量标准化，便可消除因谐波分量含量低造成各目标函数的不平衡度，使优化目标函数更合理完善。因此，这里选取：
（11） 该优化算法通过构建裕量的方程组，并引入归一化思想合理选择权重，使优化目标能综合平衡考虑各谐波误差。模型充分利用了所提取的频谱信息，弥补了频域法双端测距原理的不足，理论上可以将误差降到最低。此外，考虑到模拟退火算法能有效求解含多个未知参数的测距观测方程，因而选用该算法求解上述优化目标函数。
4.模拟退火算法
模拟退火算法优化过程由初始状态S0和控制参数初值T开始，对当前解重复“产生新解-计算目标函数差-接受或舍弃”的迭代，并逐步衰减T值，算法终止时的当前解为所得近似最优解。模拟退火算法不但接受优化解，也会以一定的概率接受非优化解[15]。随着温度的降低，系统渐渐地不再接受非优化解，并最终在温度趋于0℃的时候收敛到解状态。这种过程能够有效地避免局部搜索算法陷入局部最优的通病，是基于Mente-Carlo迭代求解策略的一种随机寻优算法。退火过程由冷却进度表（Cooling Schedule）控制，包括控制参数的初值T、衰减因子d、每个T值时的迭代次数L（马尔可夫链长度）和停止条件S。
本文选择基于模拟退火算法用Matlab求解优化模型。由于双端测距中，考虑线路参数自适应等因素及提取各谐波分量后，将使得测距观测方程未知量个数大大增加，常用的最小二乘非线性求解算法容易陷入局部最优解，尤其在处理多维、多峰值问题时，无法保证收敛于全局最优解，而模拟退火法具有全局寻优能力，不会出现陷入局部最优解而导致搜索失败的情况，并且对初值要求较低，能有效求解含多个未知参数的测距观测方程，为此，本文选择模拟退火算法求解故障测距优化模型。但由于模拟退火算法作为随机搜索算法，算法自身原理以及故障测距模型的特点决定了该算法在求解故障测距问题时仍存在计算精度不高，稳定性不足的缺点[16]。基于上述考虑，本文将已知的电缆参数作为迭代初值，利用模拟退火算法进行连续多次求解。这里选用连续五次求解出的参数作为故障距离值。
5.仿真算例及分析
5.1 PSCAD仿真
为验证所提算法的正确性和有效性，本文采用PSCAD软件对海上风电场进行三相对称接地故障的仿真，系统接线如图2所示。
仿真数据采样频率4KHz，系统参数如下：
M端系统参数：
N端系统参数：
海底电缆参数：
对故障相电缆进行短路故障仿真，两端电流电压的波形如下：
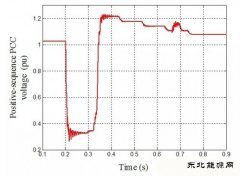
对采集到的电网侧的故障暂态电压信号进行放大，如图6所示，故障在0.02s发生，一般情况下，自由分量在故障后2个～3个周期衰减至0，即暂态自由分量的频谱主要决定于故障暂态初期的2个～3个周期[13]。从图7也可以看出，故障信号2个周期后，谐波信号几乎衰减为零，进入标准的正弦波形。为此，选择对故障信号的前两个周期进行傅里叶变换，将提取的频谱电流电压值（分别是1～4次谐波）代入优化目标函数中，在matlab软件中利用模拟退火算法进行求解。
5.2 仿真结果
在仿真模型中不断改变故障距离，记录每次的定位结果并进行分析：
其中，误差定义如下：
（12）
仿真结果由表1所示：
5.3 仿真分析
仿真结果表明以下两点：
（l）随着故障距离的增加，误差也有增大的趋势，这和求解算法有一定的关系。
（2）误差保持在2%左右，相对与线路的故障测距是较大的，但考虑到海底电缆故障测距的研究很少，算法还不成熟，这仍不失为一种较实用的定位算法。
6.结论
基于频域的优化故障定位方法非常适合海底电缆故障测距，在理论上能使测距精度非常高，误差几乎为零。但由于暂态波形提取不够完善、求解算法不够精确以及频域变换等软件上的误差，使该算法只能基本满足定位要求。不过该算法将电缆参数作为未知数求解，并引入优化算法进行优化，不受参数测量误差的影响，在目前对风电并网时海底电缆故障定位是较为实用的。
参考文献
[1]黄川.海上风电场VSC-HVDC柔性直流输电变流器研究[D].上海：上海交通大学电子信息与电气工程学院，2011.
[2]Lemming J K，Morthorst P E，Clausen N E.Offshore wind power experiences，potential and key issues for deployment[C].IEA Workshop on Offshore Wind Power；Experiences，Potentials & Key Issues for Deployment，Berlin，Germany，2007.
[3]鹿洪刚，覃剑，陈祥训等.电力电缆故障测距综述[J].电网技术，2004，28（20）：58-63.
[4]王玮，蔡伟，张元芳等.基于阻抗法的电力电缆高阻故障定位理论及试验[J].电网技术，2001，25（11）：38-41.
[5]Zhao W，Song Y H，Chen W R.Improved GPS travelling wave fault locator for power cables by using wavelet analysis[J].Electrical Power and Energy Systems，2001， 23（5）：403-411.
[6]Scutariu M.Techno-economical optioneering of offshore windfarms electrical systems//Proceedings of 2007 IEEE Lausanne Power Tech Conference，July 1-5，2007，Lausanne，Switzerland：2195-2200.
[7]张正团，文锋，徐丙垠.基于小波分析的电缆故障测距[J].电力系统自动化，2003，27（1）：49-52.
[8]张群峰，文习山，陈燕萍.基于电弧特性的电力电缆故障在线测距方法[J].高电压技术，2003，29（7）：30-31.
[9]Wedepohl L M，Wilcox D J.Transient analysis of underground power transmission systems：System-model and wave propagation characteristics[J].Proc.IEE，1973，120（2）：252-259.
[10]李骏，范春菊.基于小波分析的电缆—架空线混合输电线路行波故障测距方法[J].电网技术，2006，30（9）：92-97.
[11]于玉泽，覃剑，李功新等.电缆—架空线混合线路故障测距方法综述[J].电网技术，2006，30（17）：64-69.
[12]熊小伏，林金洪.基于小波重构的电力电缆故障测距方法[J].电网技术，2003，27（6）：36-38.
[13]安艳秋，高厚磊.基于分布参数线路模型的精确故障测距算法[J].继电器，2003，31（6）：42-45.
[14]康小宁，索南加乐.求解频域参数方程的双端故障测距原理[J].电力系统自动化，2005，29（10）：16-20.
[15]张廷龙，孙睿，胡波etal.利用模拟退火算法优化Biome-BGC模型参数[J].生态学杂志，2011，30（2）：408-414.
[16]李海锋，梁远升，王钢etal.基于模拟退火-最小二乘混合的故障测距新方法[J].电网技术，电力系统及其自动化学报，2008，20（3）：36-40.
（编辑：东北亚） |
印度计划启动首个海上
